Bir süredir dikkat mekanizmalarındaki anahtarlar, sorgular ve değerler beni de şaşırttı. Web'de arama yaptıktan ve ilgili bilgileri özümsedikten sonra, anahtarların, sorguların ve değerlerin nasıl çalıştığı ve neden işe yarayacağı hakkında net bir resme sahibim!
Nasıl çalıştıklarını ve ardından neden çalıştıklarını görelim.
Bir seq2seq modelinde, girdi dizisini bir bağlam vektörüne kodluyoruz ve ardından bu bağlam vektörünü kod çözücüye besleyerek beklenen iyi çıktı elde ediyoruz.
Ancak, giriş dizisi uzunsa, yalnızca bir bağlam vektörüne dayanmak daha az etkili hale gelir. Daha iyi kod çözme (dikkat mekanizması) için giriş sırasındaki (kodlayıcı) gizli durumlardan gelen tüm bilgilere ihtiyacımız var.
Gizli giriş durumlarını kullanmanın bir yolu aşağıda gösterilmiştir:
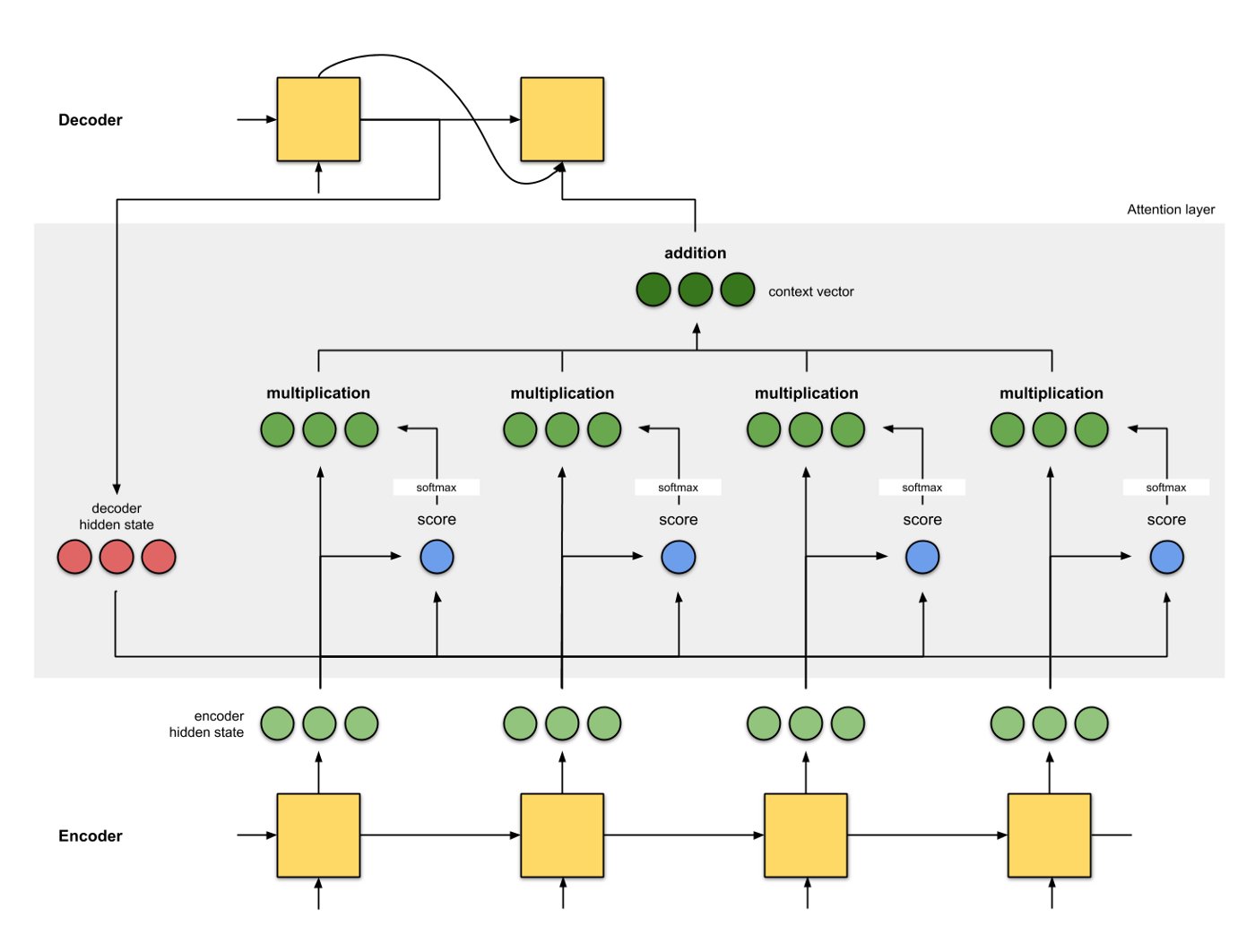 Resim kaynağı: https://towardsdatascience.com/attn-illustrated-attention-5ec4ad276ee3
Resim kaynağı: https://towardsdatascience.com/attn-illustrated-attention-5ec4ad276ee3
Başka bir deyişle, bu dikkat mekanizmasında bağlam vektörü, değerlerin ağırlıklı toplamı olarak hesaplanır; burada her bir değere atanan ağırlık, sorgunun karşılık gelen anahtarla uyumluluk işlevi tarafından hesaplanır (bu biraz [Tek İhtiyacınız Olan Dikkat] https://arxiv.org/pdf/1706.03762.pdf) sayfasından değiştirilmiş cümle.
Burada, sorgu kod çözücü gizli durumundandır, anahtar ve değer gizli kodlayıcı durumundandır (anahtar ve değer bu şekilde aynıdır). Puan, sorgu ile anahtar arasındaki uyumluluktur ve sorgu ile anahtar arasında bir iç çarpım olabilir (veya başka bir uyumluluk biçimi). Puanlar daha sonra softmax fonksiyonundan geçer ve toplamı 1'e eşit olan bir dizi ağırlık verir. Her ağırlık, tüm girdi gizli durumlarını kullanan bağlam vektörünü vermek için karşılık gelen değerlerini çarpar.
Son girdinin ağırlığını manuel olarak 1'e ve tüm önceliklerini 0'a ayarlarsak, dikkat mekanizmasını orijinal seq2seq bağlam vektör mekanizmasına indirgediğimize dikkat edin. Yani, önceki giriş kodlayıcı durumlarına hiç dikkat edilmiyor.
Şimdi, aşağıdaki şekilde gösterildiği gibi öz-ilgi mekanizmasını ele alalım:
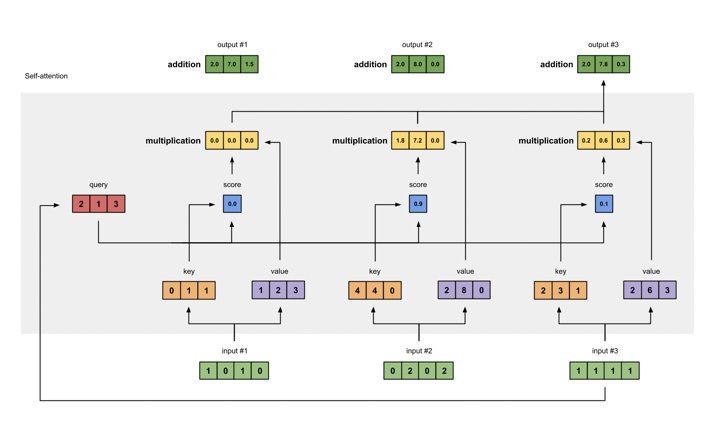 Resim kaynağı: https://towardsdatascience.com/illustrated-self-attention-2d627e33b20a
Resim kaynağı: https://towardsdatascience.com/illustrated-self-attention-2d627e33b20a
Yukarıdaki şekilden farkı, sorguların, anahtarların ve değerlerin karşılık gelen giriş durumu vektörlerinin dönüşümleri olmasıdır. Diğerleri aynı kalır.
Orijinal kodlayıcı durum vektörlerini sorgular, anahtarlar ve değerler olarak kullanmaya devam edebileceğimizi unutmayın. Öyleyse neden dönüşüme ihtiyacımız var? Dönüşüm basitçe şöyle bir matris çarpımıdır:
Sorgu = I x W (Q)
Anahtar = I x W (K)
Değer = I x W (V)
Burada I, giriş (kodlayıcı) durum vektörü ve W (Q), W (K) ve W (V), I vektörünü Sorgu, Anahtar, Değer vektörlerine dönüştürmek için karşılık gelen matrislerdir.
Bu matris çarpımının (vektör dönüşümü) faydaları nelerdir?
Aşağıdaki şekilde Tekil Değer Ayrıştırmasının (SVD) etkisini hatırlayın:

Resim kaynağı: https://youtu.be/K38wVcdNuFc?t=10
Bir giriş vektörünü bir V matrisiyle (SVD'den) çarparak, iki vektör arasındaki uyumluluğu hesaplamak için daha iyi bir temsil elde ederiz, eğer bu vektörler konu uzayında şekildeki örnekte gösterildiği gibi benzerse.
Ve bu dönüşüm matrisleri bir sinir ağında öğrenilebilir!
Kısaca, giriş vektörünü bir matrisle çarparak şunu elde ederiz:
1) giriş vektörünün daha iyi (gizli) temsili;
2) girdi vektörünün istenen boyuta sahip bir boşluğa dönüştürülmesi, örneğin boyut 5'ten 2'ye veya n'den m'ye, vb. (pratik olarak kullanışlıdır);
matrisin öğrenilebilir olduğu (manuel ayarlama olmadan).
Umarım bu, derin sinir ağlarının (kendi kendine) dikkat mekanizmasındaki sorguları, anahtarları ve değerleri anlamanıza yardımcı olur.